板书素有“微型教案”之称,它是课堂教学内容与教学过程的缩影。好的课堂板书不仅能呈现知识的形成过程,显现知识之间的内在联系,而且还能凸现教学的重难点,有利于发挥学生的思维能力。本文就数学教学中的板书设计谈几点做法和体会。
一、呈现知识的形成过程
教学过程是一个特殊的认识过程。在这个过程中,学生要经历一个从未知到已知的认识过程。数学教学不能只让学生懂得现成的数学结论,还要让学生参与知识发生、发展的过程,这才有利于学生更好地理解和掌握。课堂教学板书的设计要呈现知识的形成过程,让学生不仅知其然,还要知其所以然。如教学“分数的意义”时,是从学生生活中熟悉的平均分一个物体、一个计量单位,到把一些物体组成一个整体平均分成若干份,表示其中的一份或几份,引出分数概念的。为了把分数概念的形成过程呈现出来,可设计如下板书:
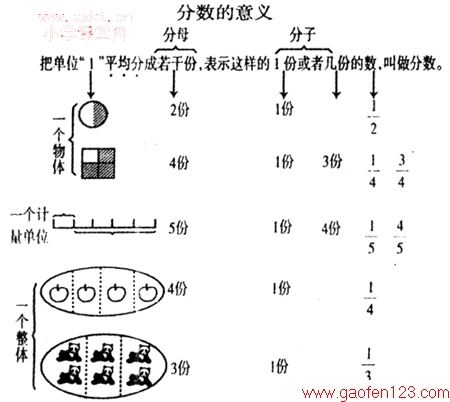
以上板书,随着学生认识的步步深入,分数的形成过程就呈现在面前,便于观察比较,舍其异取其同,把分数的共同本质特征抽取出来,从而理解和掌握分数的意义。
二、凸现教学的重难点
为了突出一堂课的教学重点,突破难点,教师要在学生保持注意的最佳时间内,结合教学活动,不惜使用一定的版面,进行板书。例如教学“一个因数是两位数的乘法”时,这一单元中“笔算乘法”的例1:每盒彩色笔24枝,13盒共有多少枝?学生列式并不困难,教学重点是因数13十位上的1乘24时,所得的数的定位问题。教学时不急于出现竖式的计算方法,可先分步列出横式:24×3、24×10,让学生口算得数,然后用竖式写出得数的位置。其方法是:把因数13分拆成10与3(即13折成整十数与一位数),分别乘以24,再求出两次乘得的数(部分积)的和。教学时板书其过程:

在此基础上指导学生写成一个竖式:

通过这样的教学及其板书,学生对两位数13乘24,即当十位上的1乘24时,得数的末位要和两位数的十位对齐的算理就清楚了。再通过“做一做”的巩固练习,学生就能自己总结出一个因数是两位数的乘法法则。
三、显现知识间的内在联系
数学是一门具有严密逻辑系统的科学,知识之间有着密切的内在联系。板书的设计要将知识间的内在联系外显出来,帮助学生完善认识结构。例如教学平面图形的面积时,随着教学进度的前进,逐步出现这些图形面积公式的推导图。在教学圆面积后,继续完成下图:
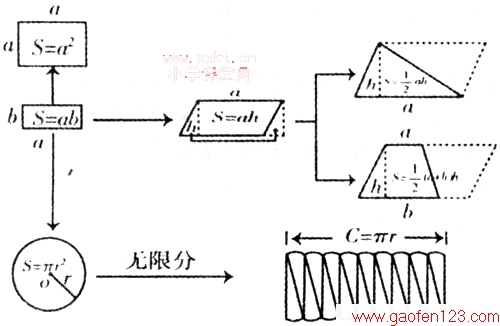
又如,教学“比与分数”“除法的关系”时,可用下列表格式的板书:

四、发展学生的思维能力
教学过程既是学生增长知识的过程,也是发展学生思维能力的过程。课堂教学中的板书是现实的,自始至终留在黑板上,使学生能边听、边看、边想、边记,多种感官参与活动,便于在观察中比较、分析、综合、抽象和概括,这对学生的思维能力,特别是逻辑思维能力的发展起着重要的作用。例如教学“小数点位置移动引起小数大小的变化”的例1时:把0.004米的小数点向右移动一位、两位、三位……小数的大小有什么变化?
0.004米=4毫米
0.04米=40毫米
0.4米=400毫米
4米=4000毫米
教学时可逐步完成下列板书:
小数点位置移动引起小数大小的变化
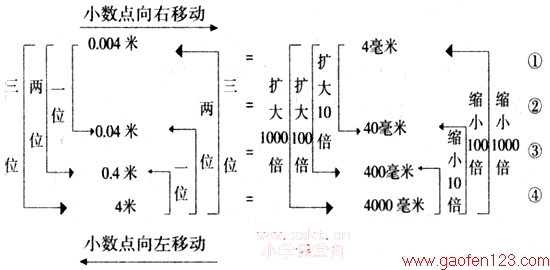
教师先引导学生对例证作整体观察:从上向下的方向顺着箭头看,小数点向右移动一位,从0.004米到0.04米,原来的4毫米变成40毫米,扩大了10倍;①式和③式比较,小数点向右移动两位,从0.004米到0.4米,原来的4毫米变成400毫米,扩大了100倍。仿此进行,让学生得出:小数点向右移动一位、两位、三位……原来的数就扩大10倍、100倍、1000倍……然后教师提出新问题:“怎样观察才能得出小数点向左移动时小数大小变化的规律?”学生运用逆向思维和类比思想找到变化规律,教师在学生回答时逐一将其板书并补充完整。这一教学过程,引导学生对例证的板书进行观察、比较、抽象、概括等,从特殊到一般归纳出知识的结论,有利于学生思维能力的发展。
此外,设计板书还要符合一些基本要求,譬如内容要主次分明,安排要疏密适宜,字体要工整规范,形式要灵活多变等,这就不一一赘述。
(选自《小学教学参考·数学版》)
上一篇:人教版课标教材三年级上册“吨的认识”案例分析
下一篇:把数学教材细节做“亮”
TAG:
+《摭谈数学教学的板书设计》相关文章
- › 摭谈数学教学的板书设计
- 在百度中搜索相关文章:摭谈数学教学的板书设计
