义务教育课程基础训练册(小学数学·二年级下册)第42页上，有这样一道换方思考题：把3、6、9、12、15、18、21、24、27这九个数填在右图1中的方格内，使每横行、竖行、斜行的三个数之和相等。
这类问题是小学数学中较难解决的问题，本文给出它的一种解法，供大家参考。
解：由每横行的三个数之和相等，可知这个相等的和数为(3+6+……+27)÷3=45。
先确定中心格内应填上什么数，暂记为“?”。由覆盖原理可知，中间横行、中间竖行及两个斜行，这些数的和应为(3+6+……+27)+?×3=45×4(中心格内的数重复了3次)，由此可得?=15。此数正好是这九个数的平均数，也是这九个数中的一个。如果此平均数不在所给出的数中，则换方无解。
接下来，是给周边格内填数。因为中心格内已填上15，且每横行、竖行、斜行的三个数之和均为45。所以，以15为中心的另两个数之和应为30。故余下的八个数只能分成以下四组：3与27，6与24，9与21，12与18。
下面，以15为中心两端填数。如果3与27填在斜行的两端上，如图2，由图易知，27所在的横行上的三个数之和与它所在的竖行上的
三个数之和中，必有一个大于45，另一个则小于45。所以，3与27不能填在四角的方格内，只能填在中间横行或中间竖行两端的方格内。
现将3与27填在中间竖行的两端方格内，如图3。27所在横行的另两个数之和只能是18，而余下的数中只有6+12=18。
当6填写在左上角的方格内，12填在右上角的方格内时，余下的填法随之而定。如图4，即为所求的一种填法。
将图4中的第一列与第三列的数对调，如图5，又是另一种不同的填法。
将图3中的3与27对调，运用上面的填法，又可得出两种不同的填法，如图6和图7。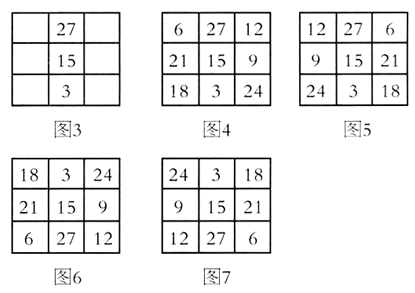
由上可
知，当3与27填在中间竖行的两端方格内时，共有四种不同的填法。
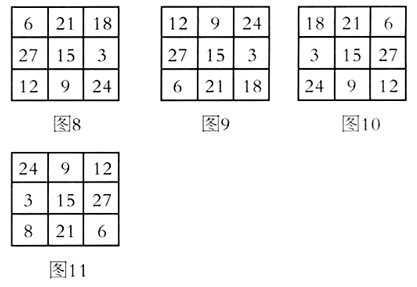
同理，当3与27填在中间横行两端的方格内时，也有四种不同的填法，如图8～图11。
综上可知，符合条件的不同填法共有八种。