小学数学教学的“小窍门”

标签：小学数学教学,http://www.gaofen123.com 小学数学教学的“小窍门”,
       人们常将教师和学生知识、能力的比假设为“1桶水”与“1杯水”，可见对教师的要求如此之高。作为教师的我们，只有平时博学善思，掌握知识的内在“窍门”，才能服务于教学，服务好学生。也就是说，只有厚积才能薄发，才能使自己在传授知识的同时有效驾驭课堂，释疑知识时游刃有余，梳理知识时高瞻远瞩，运用知识时信手拈来。
　　本文介绍几个常见的“小窍门”，供同行参考。
　　
　　1.一个合数的约数有多少个?
　　
　　学生在判断一个较大合数的约数个数(或判断写出合数的约数个数全不全)时，采用的列举法不仅麻烦，而且容易遗漏。因此，教师要教会学生巧解的方法。
　　可先将此合数分解质因数，然后看看每个质因数的最高次幂是几，再把每个次幂加1后相乘，积是多少，这个合数的约数就有多少个。如360=2×2×2×3×3×5=2³×3²×5¹，则它的约数个数是(3+1)×(2+1)×(1+1)=24(个)。(其中缘由这里不加以证明，下同)
　　
　　2.一个分数化成小数后可能是什么样的情况?
　　
　　学生在学习分数化小数时，由于受年龄和知识面的限制，经常出错且不能及时发现并纠正，造成了不应有的错误，教师应指导学生掌握以下的“窍门”。
　　首先应将这个分数化为最简分数，然后把这个最简分数的分母分解质因数，再根据分解质因数的情况加以判断：
　　(1)如果只含有2和5的质因数，则一定可以化为有限小数，且小数的位数等于质因数中2或5的最高次数。如7/40，分母40=2³×5，则7/40可化为有限小数，小数的位数是3位。
　　(2)如果只含有2和5以外的质因数，则一定可化为纯循环小数，循环节的位数不会超过这个分母的最大质因数。如7/39，分母39=3×13，不含有2或5，则7/39可化为纯循环小数，循环节的位数不超过13位。
　　(3)如果既含有2或5的质因数，又含有其他质因数，则必定化成混循环小数。不循环部分的位数是质因数中2或5的最高次数，循环节的位数不超过这个分母的最大质因数。如13/42，分母42=2×3×7，则13/42可化为混循环小数，不循环的部分有一位，第二位开始循环，且循环节的位数不超过7位。
　　
　　3、在m×n个小正方形中画一条直线，最多可以穿过多少个小正方形?
　　
　　解决此题的主要目的是发展学生的空间观念，增强学生探索规律的能力，从而使所掌握的知识在解决实际问题时发挥作用。如：怎样铺设一条直线电力线路，使尽可能多的小区受益(即成本低，效益高)?
　　
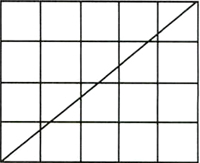
　　最多可以穿越(m+n-1)个小正方形。如上图，在5×4个的小正方形中，画一条直线，最多可以穿过5+4-1=8(个)小正方形。
　　
　　4.将两个分数的分子、分母同时扩大多少倍后，能在两个分数的中间插入多少个分母(分子)相同的分数，且使所插入的分数大于一个小于另一个？
　　
　　(1)分母(或分子)相同，分子(或分母)相差m，分子、分母扩大n倍后，则能插入(mn-1)个。如下表：
　　
　　(2)分子、分母都不同的情况，可先通分子(或分母)，再用上述方法进行。
　　当然，还可以反过来用，即由分子(或分母)相同与分母(或分子)相差几，再根据要插入的个数，确定两个分数的分子、分母同时扩大多少倍后正好能插入要求插入的个数。