互异性
一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画,可以使用多重集,其中的元素允许出现多次。
无序性
一个集合中,每个元素的地位都是相同的,元素之间是无序的。集合上可以定义序关系,定义了序关系后,元素之间就可以按照序关系排序。但就集合本身的特性而言,元素之间没有必然的序。(参见序理论)
符号表示规则
元素则通常用a,b,c,d或x等小写字母来表示;而集合通常用 A,B,C,D或X等大写字母来表示。当元素 a 属于集合 A 时,记作 a∈A。假如元素a不属于A,则记作a∉A。如果A和B两个集合各自所包含的元素完全一样,则二者相等,写作A=B。
www.gaofen123.com八、常见集合符号
N:非负整数集合或自然数集合{0,1,2,3,……}
N*或N+:正整数集合{1,2,3,……}
Z:整数集合{……,-1,0,1,……}
P:质数集合
Q:有理数集合
Q+:正有理数集合
Q-:负有理数集合
R:实数集合
R+:正实数集合
R-:负实数集合
C:复数集合
∅:空集合(不含有任何元素的集合称为空集合,又叫空集)
U:全集合(包含了某一问题中所讨论的所有元素的集合,又叫全集)
九、相关概念
元素
集合里所含有的个体称为集合的元素。例如全中国人的集合,它的元素就是每一个中国人。当x是集合A的一个元素时,可记作x∈A,读作x属于集合A。
基数
集合A中不同元素的数目称为集合A的基数,记作card(A)。当其为有限大时,集合A称为有限集,反之则为无限集。
模糊集
用来表达模糊性概念的集合,又称模糊集、模糊子集。普通的集合是指具有某种属性的对象的全体。这种属性所表达的概念应该是清晰的,界限分明的。
因此每个对象对于集合的隶属关系也是明确的,非此即彼。但在人们的思维中还有着许多模糊的概念,例如年轻、很大、暖和、傍晚等,这些概念所描述的对象属性不能简单地用“是”或“否”来回答,模糊集合就是指具有某个模糊概念所描述的属性的对象的全体。
由于概念本身不是清晰的、界限分明的,因而对象对集合的隶属关系也不是明确的、非此即彼的。这一概念是美国加利福尼亚大学控制论专家L.A.扎德于 1965 年首先提出的。
模糊集合这一概念的出现使得数学的思维和方法可以用于处理模糊性现象,从而构成了模糊集合论(中国通常称为模糊性数学)的基础。
幂集
定义:设有集合A,由集合A所有子集组成的集合,称为集合A的幂集。
定理:有限集A的幂集的基数等于2的有限集A的基数次方。
并、交集
并集定义:由所有属于集合A或属于集合B的元素所组成的集合,记作A∪B(或B∪A),读作“A并B”(或“B并A”),即A∪B={x|x∈A,或x∈B}。并集越并越多。
交集定义:由属于A且属于B的相同元素组成的集合,记作A∩B(或B∩A),读作“A交B”(或“B交A”),即A∩B={x|x∈A,且x∈B}。交集越交越少。
若A包含于B,则A∩B=A,A∪B=B
补集
相对补集定义:由属于A而不属于B的元素组成的集合,称为B关于A的相对补集,记作A-B,即A-B={x|x∈A,x∉B'}
绝对补集定义:A关于全集合U的相对补集称作A的绝对补集,记作A'或?u(A)或~A。·U'=Φ;Φ‘=U
十、运算
交换律:A∩B=B∩A A∪B=B∪A
结合律:A∪(B∪C)=(A∪B)∪C A∩(B∩C)=(A∩B)∩C
分配对偶律:A∩(B∪C)=(A∩B)∪(A∩C) A∪(B∩C)=(A∪B)∩(A∪C)
对偶律:(A∪B)^C=A^C∩B^C (A∩B)^C=A^C∪B^C
同一律:A∪Φ=A A∩U=A
求补律:A∪A'=U A∩A'=Φ
对合律:(A')'=A
等幂律:A∪A=A A∩A=A
零一律:A∪U=U A∩U=A
吸收律:A∪(A∩B)=A A∩(A∪B)=A
德·摩根定律(反演律):(A∪B)'=A'∩B' (A∩B)'=A'∪B'
德摩根律:1.集合A与集合B的交集的补集等于集合A的补集与集合B的补集的并集; 2.集合A与集合B的并集的补集等于集合A的补集与集合B的补集的交集。 容斥原理(特殊情况):card(A∪B)=card(A)+card(B)-card(A∩B)
card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(B∩C)-card(C∩A)+card(A∩B∩C)
容斥原理基本思想:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
【练习题】
1、下列四组对象,能构成集合的是( )
A.某班所有高个子的学生 B.著名的艺术家 C.一切很大的书 D.倒数等于它自身的实数
2、集合{a,b,c }的真子集共有( )个
A.7 B.8 C.9 D.10
3、点的集合M={(x,y)|xy≥0}是指( )
A.第一象限内的点集 B.第三象限内的点集
C.第一、第三象限内的点集 D.不在第二、第四象限内的点集
4、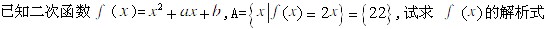
5、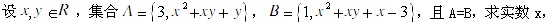 y的值
y的值
【参考答案】
1、D
2、A
3、D
4、

5、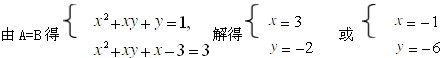
+《集合概念、知识点及练习题》相关文章
- › 集合概念、知识点及练习题
- 在百度中搜索相关文章:集合概念、知识点及练习题
