关键是数学思想方法
名师介绍:
周洁珍,华南师范大学附属中学数学一级教师
2010年~2012年近三年来的广州市中考数学试卷结构都比较稳定,试题依据课标和考纲,全面考查考试大纲中基础知识点,重点考查初中数学的核心内容,如函数、方程与不等式、三角形、四边形、圆、概率与统计等。试卷注重基础,难易有度,具有以下特点:
1. 考试时间都是120分钟;
2.题型的分布都是选择题10道(30分),填空题6道(18分),解答题9道(102分),总共25道题(150分);
3.试卷难度不大,前22题均为学生熟悉的常规性试题,共计122分(占全卷满分的82%),后3题为中高档题,共计28分(占全卷满分的18%);试卷同时渗透了初中数学中常见的函数与方程、数形结合、分类讨论、运动变化、待定系数法等数学思想方法。
接下来重点介绍综合能力考察与应用部分这部分的中考数学试题。
实践与综合应用部分又被大家称为“压轴题”,压轴综合题在近年广州市中考题中都出现在24、25题,分值为28分,难度较大,作为压轴题,所覆盖的知识点是最全面,能力要求最高,灵活性最强的问题。一类是以几何图形的变化为主线的;另一类是以函数图像知识考察为主线的,大致有以下五种类型:
(1)从数量角度反映变化规律的函数类题型:
(2)以直角坐标系为载体的几何类题型:
(3)以“几何变换”为主体的几何类题型:
(4)以“存在型探索性问题”为主体的综合探究题:
(5)以“动点问题”为主的综合探究题:
例题:(2012年广州市)24.(本小题满分14分)
如图9,抛物线

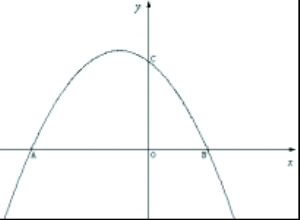
与轴交于A、B两点(点A在点B的左侧),与轴交于点C
(1) 求点A、B的坐标;
(2)设D为已知抛物线对称轴上任意一点,当ACD面积等于ACB面积时,求点D的坐标;
(3)当直线l过点(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式。
分析:
(1) A、B点为抛物线与x轴交点,令y=0,解一元二次方程即可.
(2)根据题意求出ACD中AC边上的高,设为h.在坐标平面内,作AC的平行线,平行线之间的距离等于h.根据等底等高面积相等,可知平行线与坐标轴的交点即为所求的D点。
从一次函数的观点来看,这样的平行线可以看做是直线AC向上或向下平移而形成.因此先求出直线AC的解析式,再求出平移距离,即可求得所作平行线的解析式,从而求得D点坐标.
注意:这样的平行线有两条,如答图1所示。
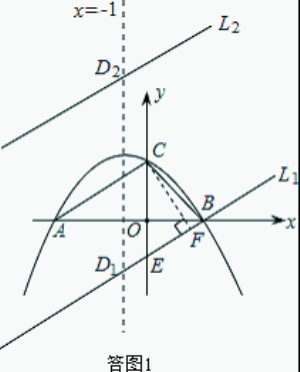
(3) 本文关键是理解“以A、B、M为顶点所作的直角三角形有且只有三个”的含义。
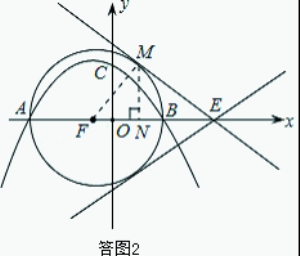
因为过A、B点作x轴的垂线,其与直线l的两个交点均可以与A、B点构成直角三角形,这样已经有符合题意的两个直角三角形;第三个直角三角形从直线与圆的位置关系方面考虑,以AB为直径作圆,当直线与圆相切时,根据圆周角定理,切点与A、B点构成直角三角形.从而问题得解。
注意:这样的切线有两条,如答图2所示。
+《中考数学冲刺在即同学策马扬鞭》相关文章
- › 中考数学复习:记准定理推论
- › 中考数学冲刺在即同学策马扬鞭
- › 中考数学复习有效学习方法
- › 中考数学高分指导:几何函数题目不断“重复
- › 中考数学之如何考前准备
- › 中考数学25题,题型练习
- 在百度中搜索相关文章:中考数学冲刺在即同学策马扬鞭
